|
The Earth’s magnetopause is the result of the interaction between the supersonic solar wind and the Earth’s magnetic field. It basically separates the interplanetary magnetic field from the Earth’s magnetic field and prevents most solar wind plasma from entering the Earth’s magnetosphere. It adjoins the low-latitude boundary layer, the entry layer, the cusp and the plasma mantle [Eastman et al., 2000; Phan et al., 1997]. It is also the place where the reconnection occurs with the mass, energy and momentum transfer from the magnetosheath into the magnetosphere. 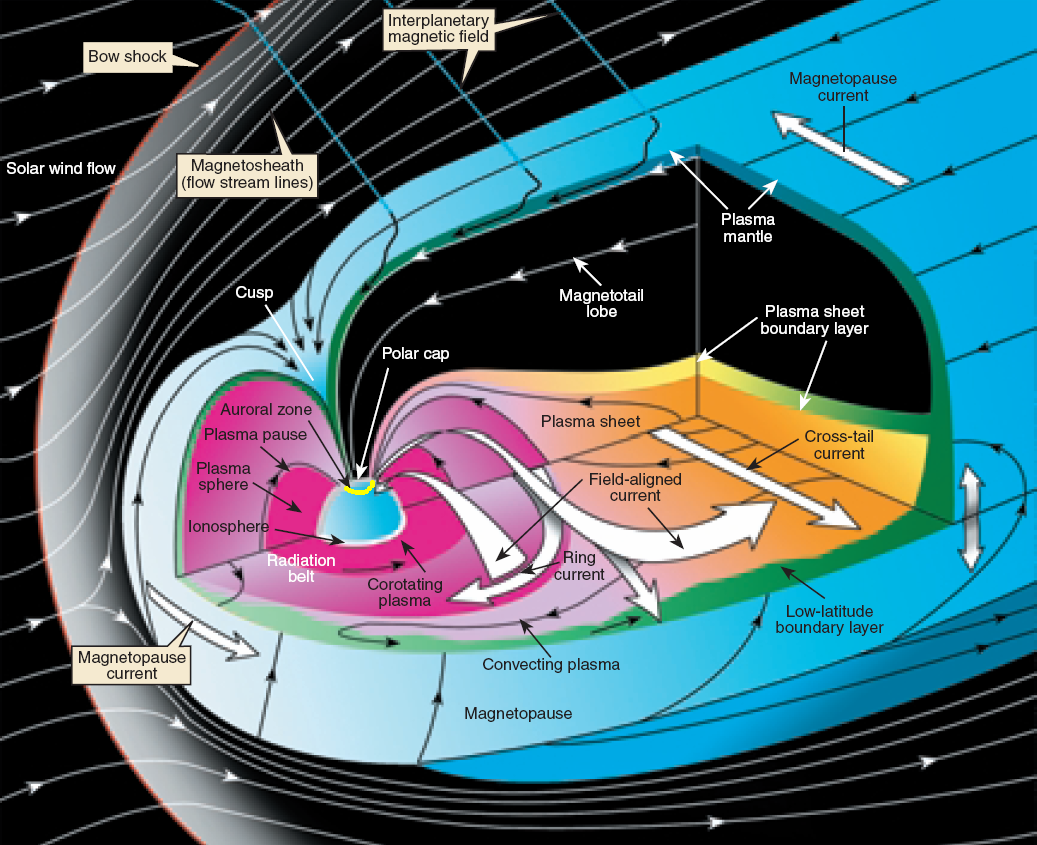 Previous theoretical and statistical studies indicate that the global structure of the magnetopause is greatly influenced by the solar wind plasma and the interplanetary magnetic field. Under varying solar wind conditions, the magnetopause subsolar distance, r0, can be changed from 5.2 Re to 14 Re [Kuznetsov and Suvorova, 1998]. When r0 is less than 6.6 Re, geosynchronous satellites may cross the magnetopause and experience anomalies such as attitude and angular momentum control distortion [Shue et al., 2001]. Therefore, the prediction of the magnetopause size and shape is important not only for theoretical research and numerical simulation, but also for space weather applications. 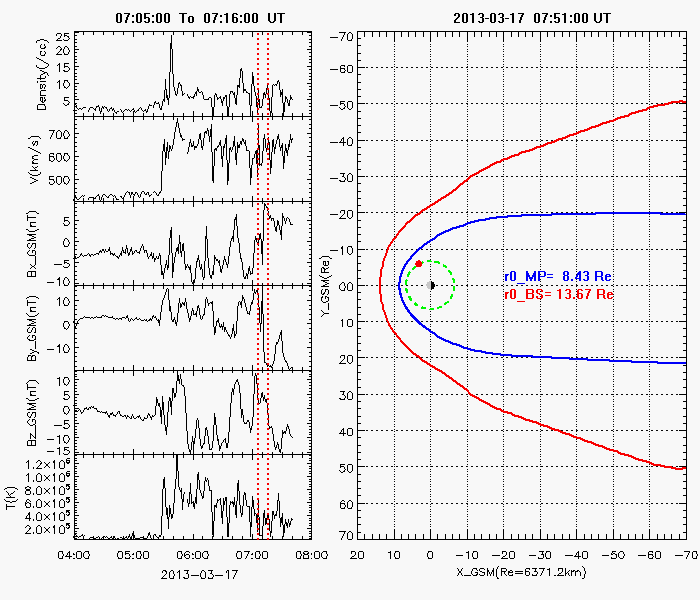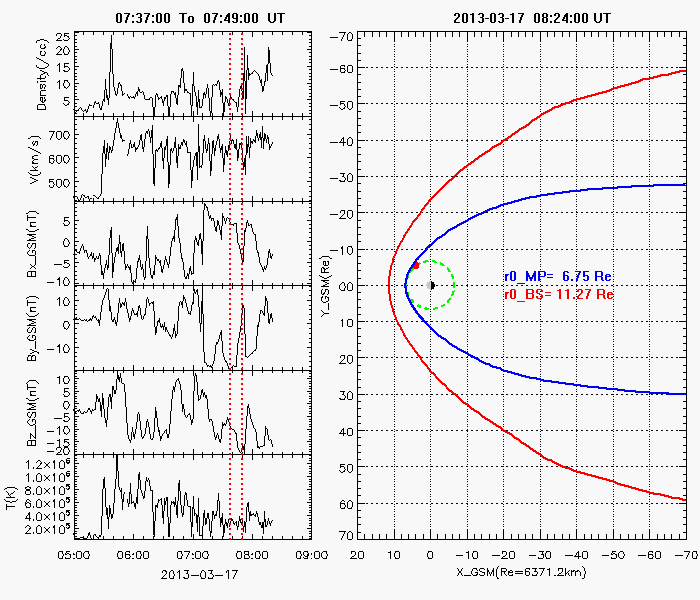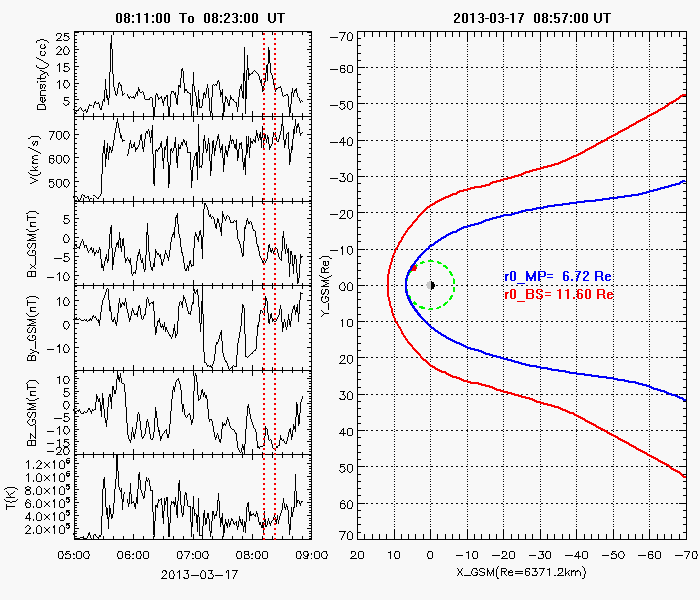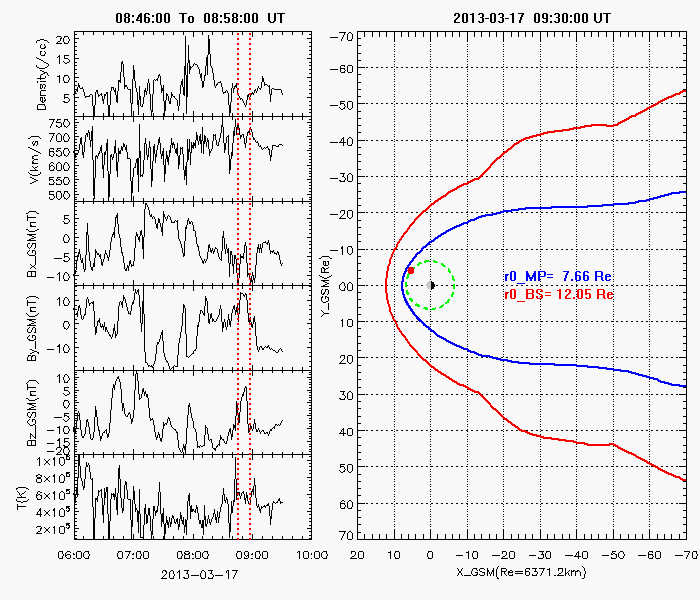 Various empirical magnetopause models have been developed in the past decades [Fairfield, 1971; Howe et al., 1972; Holzer and Slavin, 1978; Formisano et al., 1979; Petrinec et al., 1991; Sibeck et al., 1991; Roelof and Sibeck, 1993; Petrinec and Russell, 1993, 1996; Kuznetsov and Suvorova, 1996; Shue et al., 1997, 1998; Kuznetsov and Suvorova, 1998; Kawano et al., 1999; Boardsen et al., 2000; Kalegaev and Lyutov, 2000; Chao et al., 2002]. Most of them were developed mainly based on low-latitude magnetopause crossings with the rotationally symmetric assumption and parameterized by the solar wind dynamic pressure (Pd) and/or the interplanetary magnetic field (IMF) Bz. These rotationally symmetric models often use an elliptic function, a parabolic function or the Shue model function as a basic functional form to describe the magnetopause. In order to overcome the limit of an elliptic function, which must cross at some point on the nightside and can’t represent the distant tail magnetopause [Slavin et al., 1985], Petrinec and Russell [1996] used the inverse trigonometric functions to describe the nightside magnetopause and Kawano et al. [1999] used a cylinder to represent the tail magnetopause from the position where its transverse radius () reaches the maximum. The Shue model function has the flexibility to produce an open or closed magnetopause and has a reasonable extrapolation ability to predict the distant tail magnetopause. In addition, the saturation influence of southward IMF BZ on is also considered in the Shue et al. [1998] model and the Kuznetsov and Suvorova [1998] model. It is noted that the Petrinec and Russell [1996] model, the Shue et al. [1998] model and the Chao et al. [2002] model have an appropriate capability to forecast geosynchronous satellites crossing the magnetopause under extreme solar wind conditions [Yang et al., 2002]. For the high-latitude region, Formisano et al. [1979] constructed an average magnetopause size and shape in SM coordinates for two dipole tilt angle () values. Boardsen et al. [2000] developed a quantitatively empirical high-latitude magnetopause model parameterized by Pd, IMF Bz and for corrected GSM coordinates based on the northern hemisphere magnetopause crossings. Boardsen et al. [2000] did not fully model the three-dimensional magnetopause indentation due to the limitation of model functions. This model is only valid near the subsolar region and at high latitudes in the near-Earth region with XGSM ≥ -5 Re and not appropriate for the low latitudes away from the subsolar region. Obviously, these available magnetopause models are not very satisfactory to describe the global magnetopause structure, as shown in Figure 3, because of the limitation of their model functions. Fortunately, we found the advantage of Shue model function, and developed it into a three-dimensional global magnetopause model function, able to describe the asymmetries and the indentations of the magnetopause. Based on this model function, the magnetopause crossings from Geotail, IMP8, Interball, TC1, THEMIS, Wind, Cluster, Polar, LANL, GOES and Hawkeye, and the Levenberg-Marquardt fitting method, a new three-dimensional asymmetric magnetopause model was developed for corrected GSM coordinates and parameterized by the solar wind dynamic and magnetic pressures (Pd+Pm), the interplanetary magnetic field (IMF) Bz, and the dipole tilt angle. The asymmetries of the magnetopause and the indentations near the cusps are appropriately described in this new model, as shown in Figure 4. In addition, the saturation effect of IMF Bz on the subsolar distance and the extrapolation for the distant tail magnetopause are also considered. In comparison with the previous empirical magnetopause models based on our database, the new model improves prediction capability to describe the three-dimensional structure of the magnetopause. It is shown that this new model can be used to quantitatively study how Pd+Pm compresses the magnetopause, how the southward IMF Bz erodes the magnetopause, and how the dipole tilt angle influences the north-south asymmetry and the indentations. 
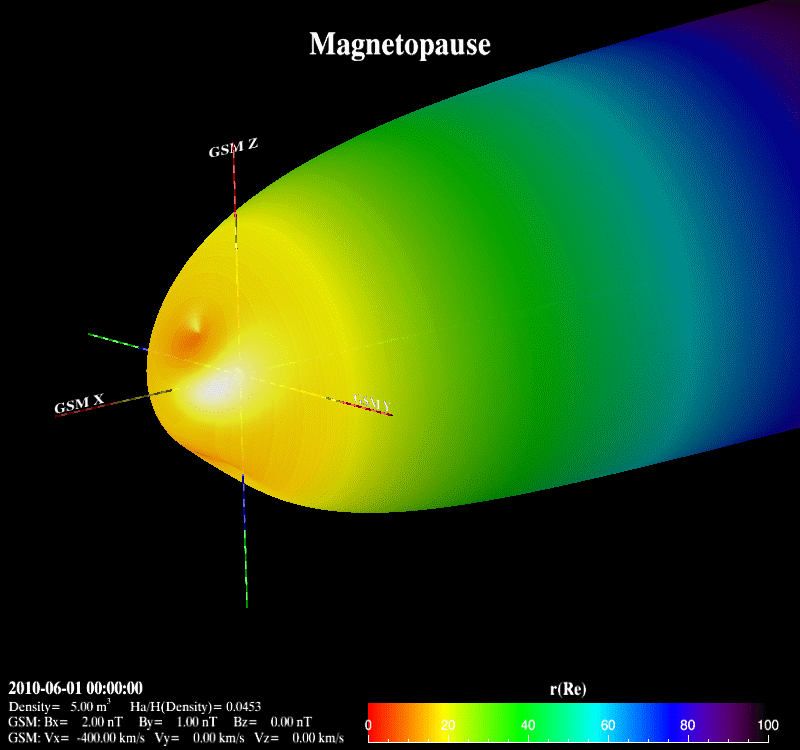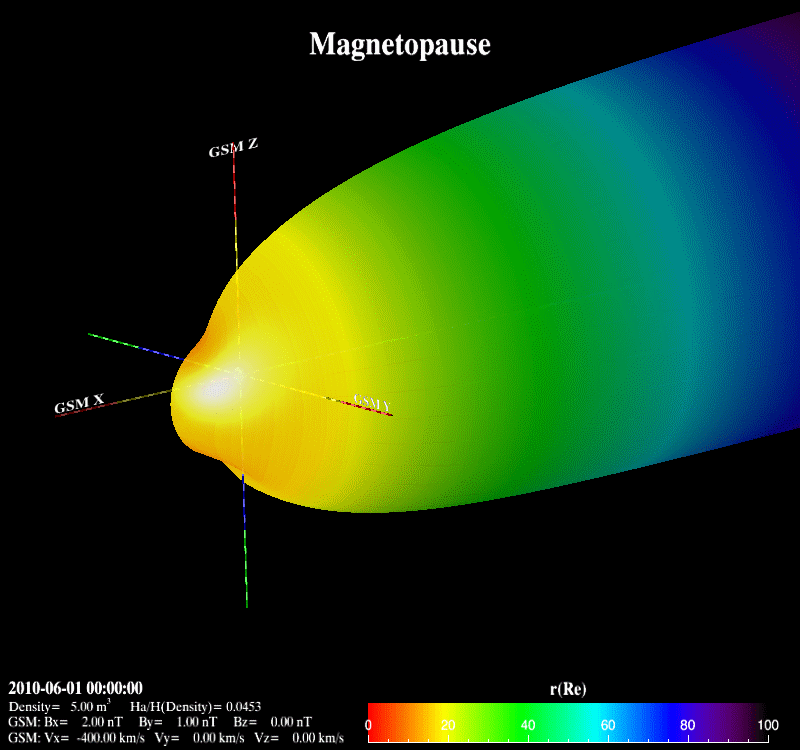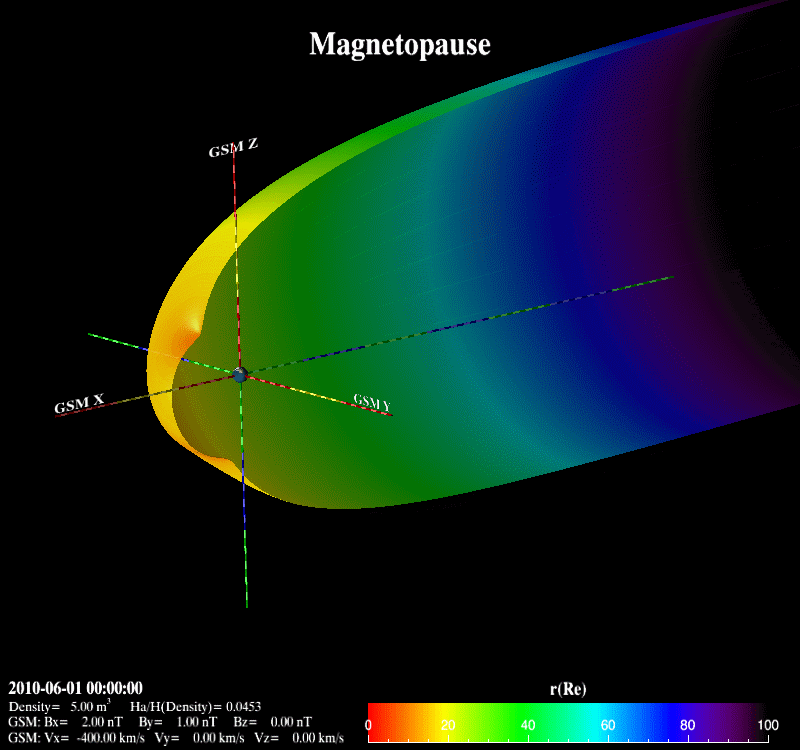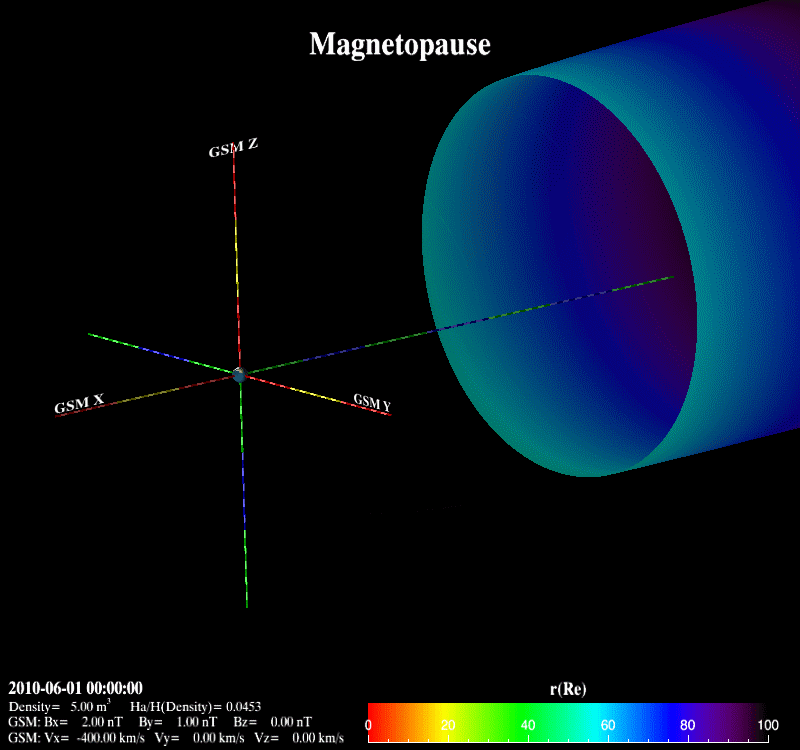 Lin, R. L., et al (2010), A three-dimensional asymmetric magnetopause model, J. Geophys. Res., 115, A04207, doi:10.1029/2009JA014235. |
Earth's Magnetopause and Bow Shock









